【算法】回溯算法

算法深度优先搜索回溯法二维数组

Algorithm

发布日期: 2021-07-02

文章字数: 2.5k

阅读时长: 10 分

阅读次数:

回溯算法

定义

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。因此回溯算法用于搜索一个问题的所有解，通过深度优先遍历的思想实现。

解题步骤

首先应该先明确定义问题的解空间，其至少包含问题的一个解
确定结点的扩展搜索规则
以深度优先的方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索
- 回溯算法会应用剪枝技巧加快搜索速度。有些时候，需要一些预处理才能达到剪枝的目的。

回溯算法的题型

排列，组合，子集等问题
解题的步骤是：先画图，再编码。去思考可以剪枝的条件，为什么有的时候用 state 数组，有的时候设置搜索起点start变量，理解状态变量设计的想法。

矩阵搜索相关问题

字符串中回溯问题
字符串的问题的特殊之处在于，字符串的拼接生成新对象，因此在这一类问题上没有显示「回溯」的过程

游戏问题

问题举例

排列组合问题

77.组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合
输入: n = 4, k = 2
输出:[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4]]

解题思路
如果给出n = 3； k = 2，那么递归结构就为：

如果组合里有 1 ，那么需要在 [2, 3] 里再找 1 个数
如果组合里有 2 ，那么需要在 [3] 里再找 1数。这里不能再考虑 1，因为包含1的组合，在第1种情况中已经包含。
以此类推，在以 n结尾的候选数组里，选出若干个元素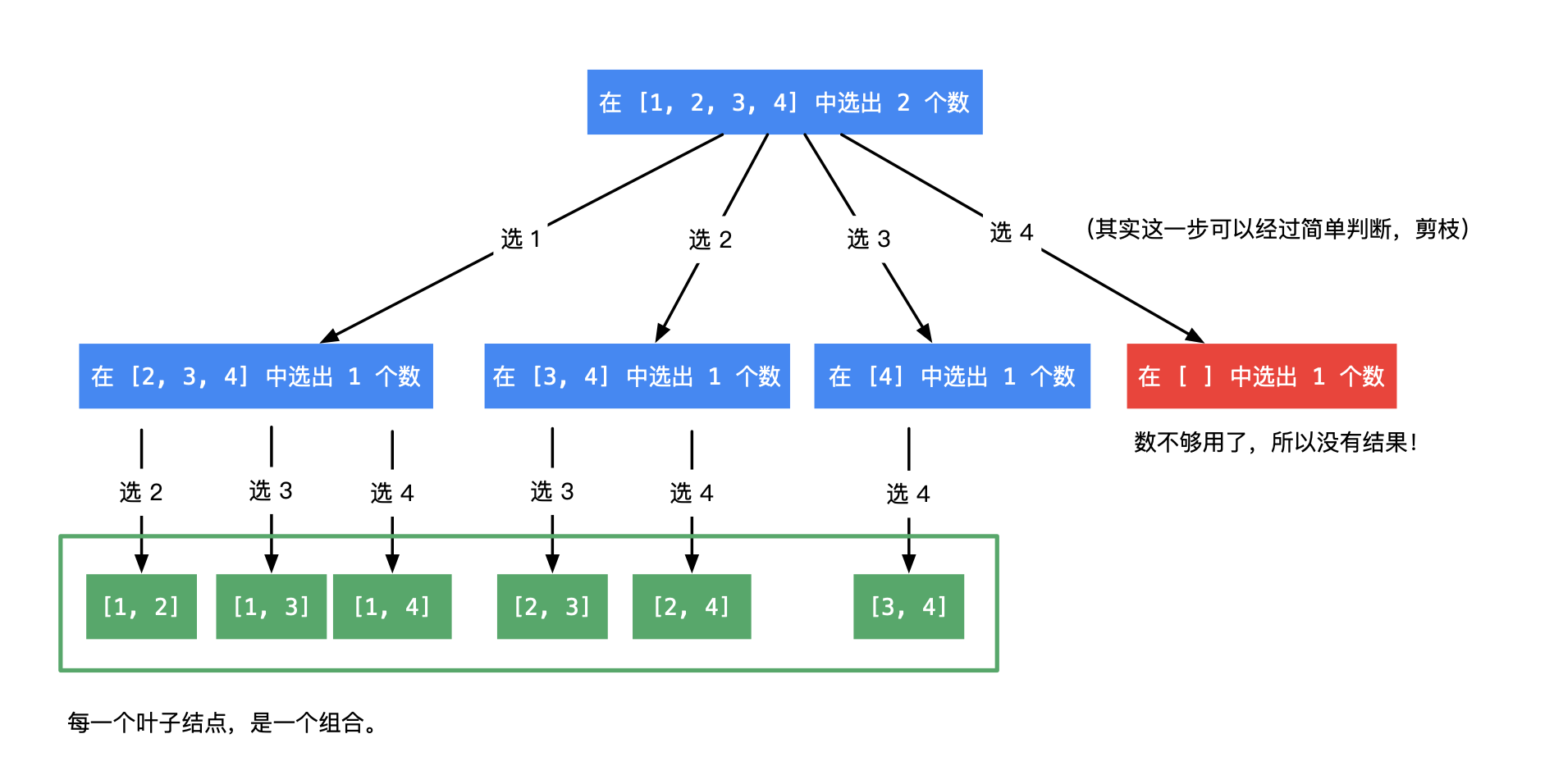

引用weiwei大神的图

在遍历树中，叶子结点的信息体现在从根结点到叶子结点的路径上，因此需要一个表示路径的变量 path

每一个结点递归地在做同样的事情，区别在于搜索起点，因此需要一个变量 begin ，表示在区间 [begin, n] 里选出若干个数的组合

class Solution {
public:
    vector<int> path;
    //将path数组和res结果数组为成员变量，减少调用参数
    vector<vector<int>> res;  
    vector<vector<int>> combine(int n, int k) {
        dfs(n, k, 1);
        return res;
    }

    void dfs(int n, int k, int start)
    {	//如果path长度满足k，则加入进res中
        if(path.size() == k)	
        {
            res.push_back(path);
            //并返回上一个结点
            return;				
        }

        for(int i = start; i <= n; i++)
        {
            path.push_back(i);	//将结点加入path中
            //递归地搜索，注意进入下一个递归时，应该从下一个数字，避免重复进入
            dfs(n, k, i+1);		
            //回溯，将此节点弹出，进入下一个循环
            path.pop_back();	
        }
    }
};

下面一副流程图可以加深对递归过程的理解（跟着箭头的流程）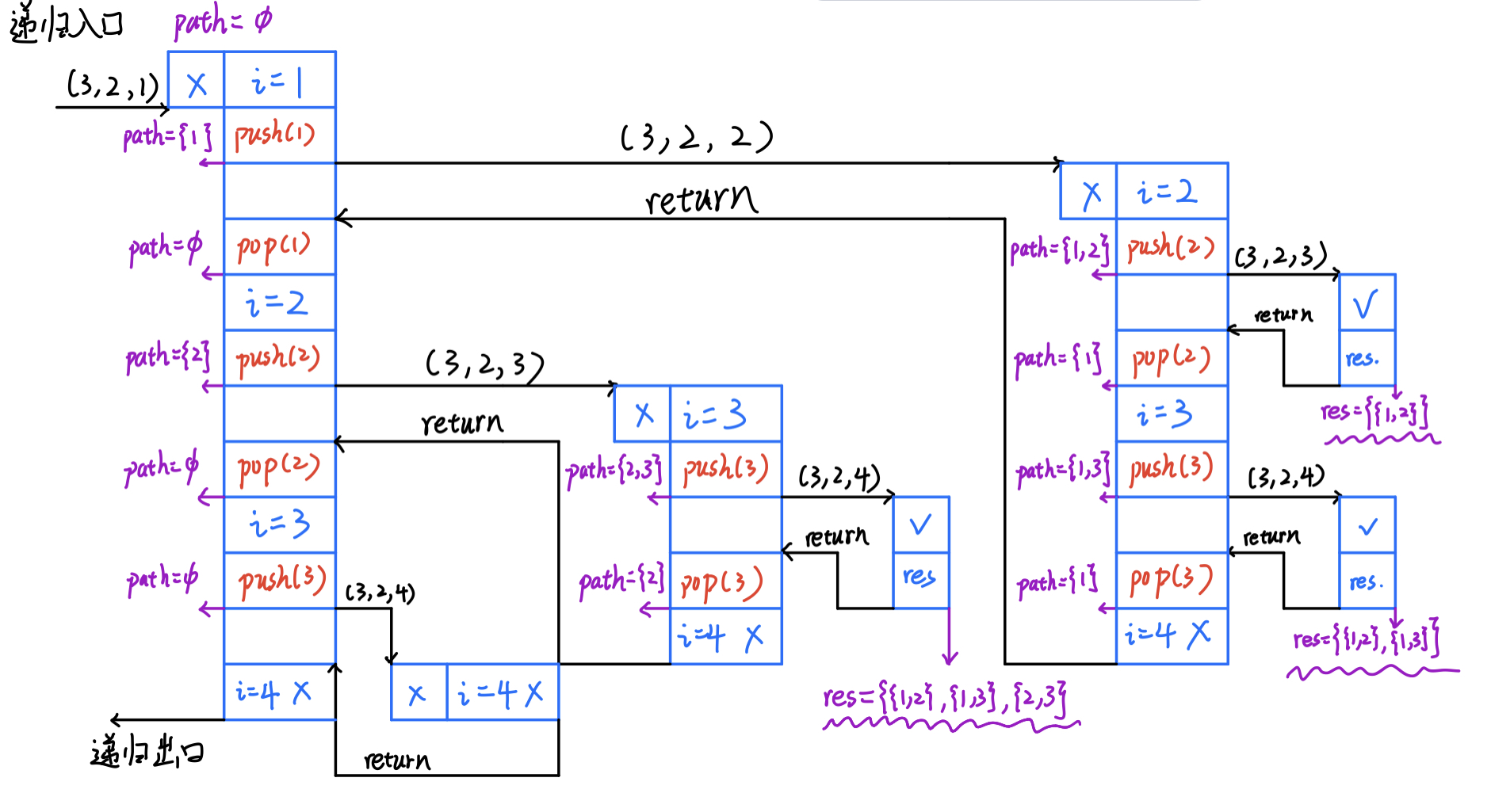
递归流程图

47.全排列

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。
输入：nums = [1,1,2]
输出：[[1,1,2],[1,2,1],[2,1,1]]

思路：
首先对于没有重复数字数组的全排列，我们采用了一个state数组来表示当前元素是否被选用过，来进行重复项的剪枝，但本题中有重复数字，所以在结果集中必然包含重复项。
(例如[1,1,2]的结果集为[1,1’,2], [1,2,1’], [1’,1,2], [1’,2,1], [2,1,1’], [2,1’,1])
所以有两种思路容易想到：

在结果集中去重
在遍历的过程中，一边遍历一遍检测，在一定会产生重复结果集的地方剪枝。
然而结果集是数组集合，去重比较麻烦，所以采用剪枝的办法，在遍历过程中直接去重。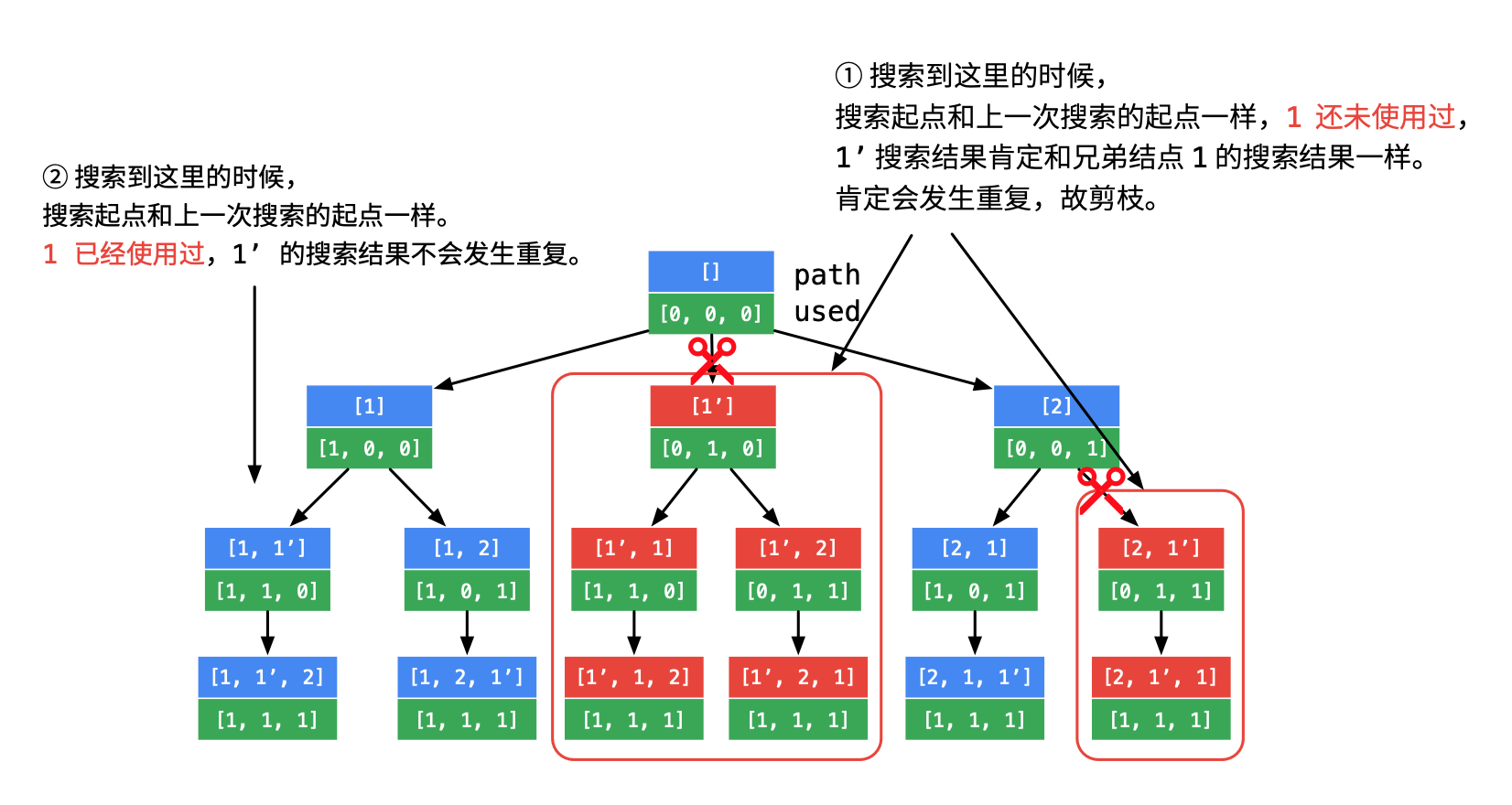

再次引用weiwei大神的图

在图中 ② 处，搜索的数也和上一次一样，但是上一次的 1 还在使用中；

在图中 ① 处，搜索的数也和上一次一样，但是上一次的 1 刚刚被撤销，正是因为刚被撤销，下面的搜索中还会使用到，因此会产生重复，剪掉的就应该是这样的分支。

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;		//同上
    vector<vector<int>> permuteUnique(vector<int>& nums) {
    	//排序保证重复项相邻
        sort(nums.begin(), nums.end());		
        //state数组表示元素是否被用
        vector<int> state(nums.size(), 0);	
        dfs(nums, state);
        return res;
    }

    void dfs(vector<int>& nums, vector<int>& state)
    {
    	//path长度满足加入res
        if(path.size() == nums.size())		
        {
            res.push_back(path);
            return;
        }
		 //i从0开始，每层递归都从首项开始遍历
        for(int i = 0; i < nums.size(); i++)
        {
        	//先判断是否使用过
            if(state[i] == 1)				
            {
                continue;
            }
            //判断是否重复并且上一个元素被弹出（这样才保证了i元素不取）
            if(i > 0 && nums[i] == nums[i - 1] && state[i-1] != 1)
            {
                continue;
            }
            //加入path
            path.push_back(nums[i]);	
            //将此元素状态设为用过再进行递归
            state[i] = 1;				
            dfs(nums, state);
            //弹出
            path.pop_back();
            //将状态设为未用过后进入下一个循环
            state[i] = 0;				
        }
    }
};

矩阵搜索相关问题

79.单词搜索I

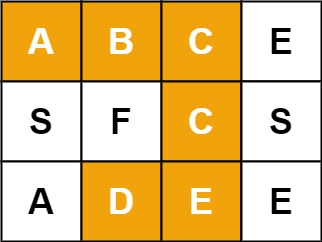
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

思路：
使用深度优先搜索（DFS）和回溯的思想实现。关于判断元素是否使用过，将使用过的元素赋值为“#”，再返回上一个结点时重置

class Solution {
public:
    
    bool find = false;
    bool exist(vector<vector<char>>& board, string word) {
        int m = board.size();
        int n = board[0].size();
		//先暴力搜索找到第一个与word[0]相同的位置
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(board[i][j] == word[0])
                {
               		//找到后进入递归，从第0个元素开始
                    dfs(board, word, i, j, 0);
                }
            }
        }

        return find;
    }

    void dfs(vector<vector<char>>& board, string word, int i, int j, int index)
    {	如果index与word长度相同时返回true（不是size-1的理由：当最后一个字母匹配成功(index = size-1)的时候，dfs并未结束，而是会再一次进入递归，此时再判断才能满足完全匹配）
        if(index == word.size())
        {
            find = true;
            return;
        }
        //超出界限或者与word[index]不匹配，则返回上一个结点
        if(i < 0 || i >= board.size() || j < 0 || j >= board[0].size() || board[i][j] != word[index])
        {
            return;
        }
		//记录此时board[i][j]
        char temp = board[i][j];
        //将board[i][j]重置为#表示遍历过
        board[i][j] = '#';
		//向四个方向进行dfs
        dfs(board, word, i + 1, j, index + 1);
        dfs(board, word, i - 1, j, index + 1);
        dfs(board, word, i, j + 1, index + 1);
        dfs(board, word, i, j - 1, index + 1);
        //将board[i][j]重置为原来的数
        board[i][j] = temp;
    }

};

字符串相关回溯问题

17.电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

思路：
本题思路和组合问题基本一致，只是多了一个数字与字母的映射条件，要做的就是建立一个哈希表储存映射，进行深度搜索时要注意各个参数所代表的意义。

class Solution {
public:
	//哈希映射，储存数字与字母的映射
    unordered_map<char, string> m=
    {
        {'2', "abc"},
        {'3', "def"},
        {'4', "ghi"},
        {'5', "jkl"},
        {'6', "mno"},
        {'7', "pqrs"},
        {'8', "tuv"},
        {'9', "wxyz"}
    };
    //临时储存字符串的变量
    string path;
    //储存结果的数组，声明为成员变量，减少传入的参数
    vector<string> res;
    vector<string> letterCombinations(string digits) {
        dfs(digits, 0);
        return res;        

    }
    void dfs(string digits, int index)
    {
    	//如果path长度满足加入res
        if(path.size() == digits.size())
        {
            res.push_back(path);
            return;
        }
        //此时index的意义为digit[index]所对应的值在哈希表中所映射的字符串
        //比如digits[2]为'3'，那么temp为"def";
        string temp = m[digits[index]];
        //从头开始遍历，因为递归过程改变的时temp，所以要保证temp中所有字母都被取到
        for(int i = 0; i < temp.size(); i++)
        {
        	//+一个字母
            path += temp[i];
            //继续递归，并遍历digits的下一个数字
            dfs(digits, index + 1);
            //弹出path的最后一个字母，和组合一样
            path.pop_back();
        }

    }
};