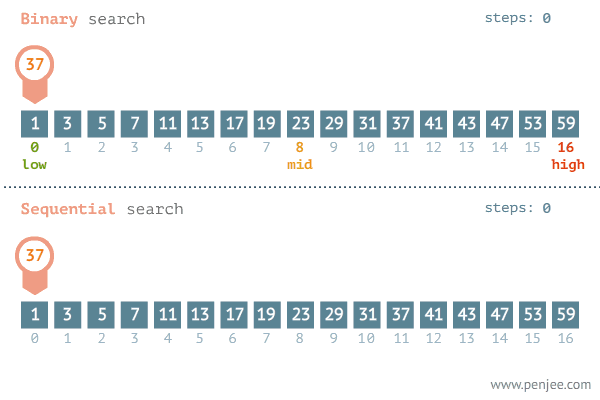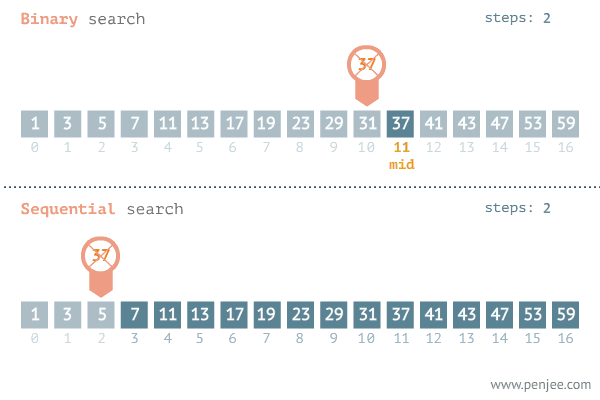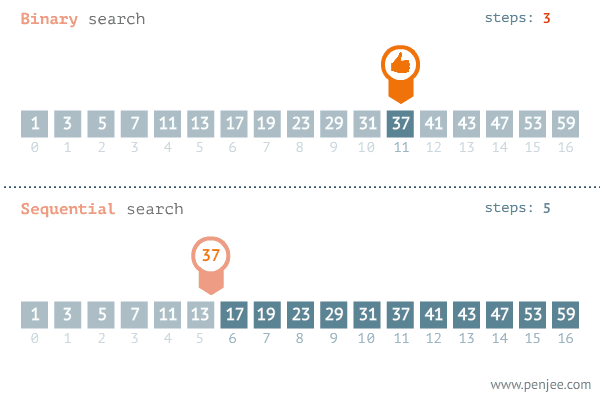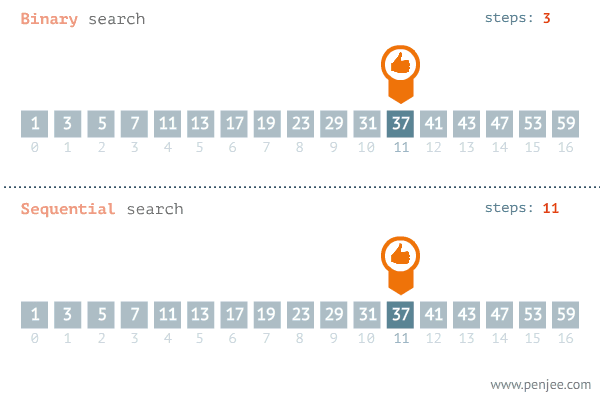
二分查找
二分查找也称折半查找(Binary Search),是一种在有序数组中查找某一特定元素的搜索算法。我们可以从定义可知,运用二分搜索的前提是数组必须是有序的,这里需要注意的是,我们的输入不一定是数组,也可以是数组中某一区间的起始位置和终止位置。
二分法两种写法的对比
- while(left <= right)
退出循环的时候,right 在左,left 在右,区间为空区间,所以要讨论返回 left 和 right。 - while(left < right)
退出循环的时候,left 与 right 重合,区间里只有一个元素。
二分法的题型
完全有序数组中查找
35. 搜索插入位置
34. 在排序数组中查找元素的第一个和最后一个位置
4. 寻找两个正序数组的中位数
69. x 的平方根(二分法的变种应用)不完全有序数组中查找
33. 搜索旋转排序数组
81. 搜索旋转排序数组 II
153. 寻找旋转排序数组中的最小值
154. 寻找旋转排序数组中的最小值 II二维数组中查找
74. 搜索二维矩阵
240. 搜索二维矩阵 II
二分法基本用法
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = nums.size();
int left = 0;
int right = n - 1;
while(left <= right)
{
//使用这种方式防止left+right溢出(超出整数范围)
int mid = left + (right - left) / 2;
//小了就取右边区间
if(nums[mid] < target)
{
left = mid + 1;
}
//大了就取左边区间
else if(nums[mid] > target)
{
right = mid - 1;
}
else
{
return mid;
}
}
return -1;
}
};问题举例
完全有序数组中查找
34. 在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target,返回 [-1, -1]。
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
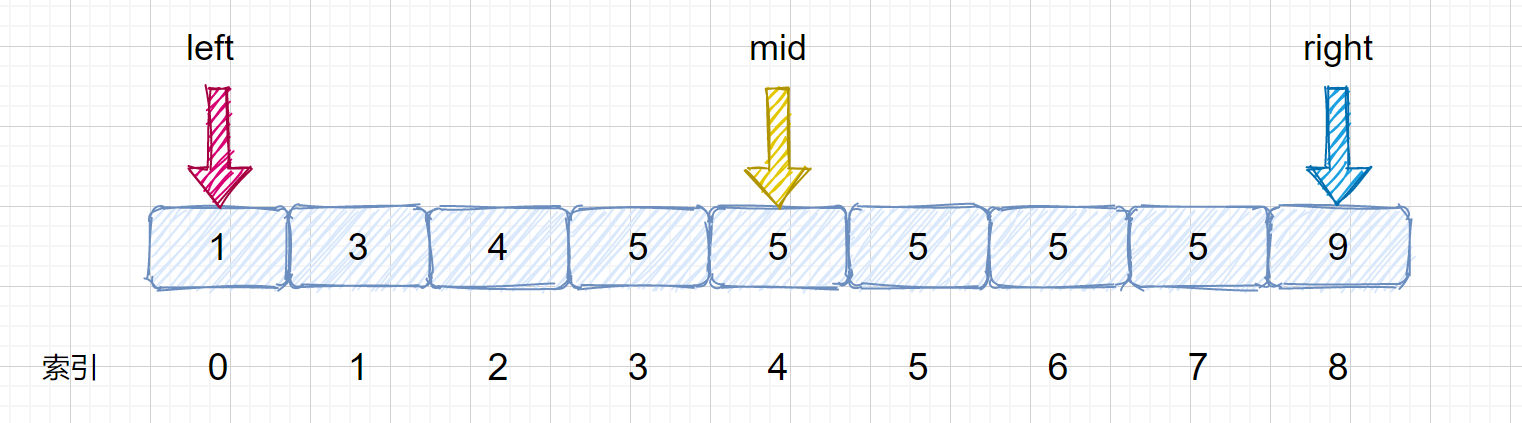
思路:如果此时我们的 nums[mid] = target ,但是不能确定 mid 是否为该目标数的左边界或者右边界。所以分为两种情况,先找左边界,再找右边界。
- 左边界: 如上图所示,当找到target时不能直接返回,而是继续查找。只需在target <= nums[mid]时,让right = mid - 1即可,这样就可以继续在mid的左区间继续寻找
- 右边界:同理,target >= nums[mid]时,让left = mid + 1即可,这样就可以继续在mid的右区间继续寻找
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int n = nums.size();
int l = 0;
int r = n - 1;
int i = -1;
int j = -1;
//寻找左边界
while(l <= r)
{
int mid = l + (r - l) / 2;
//如果num[mid]>=target的话就一直在左区间查找
if(nums[mid] >= target)
{
r = mid - 1;
}
else
{
l = mid + 1;
}
}
//如果l超出范围或者没有找到目标值,则直接返回{-1,-1}
if(l < 0 || l >= n)
{
return {i, j};
}
if(l >= 0 && nums[l] != target)
{
return{i, j};
}
//退出循环时,l恰好在左边界的位置
i = l;
//将边界重置
l = 0;
r = n - 1;
//寻找右边界
while(l <= r)
{
int mid = l + (r - l) / 2;
//如果num[mid]<=target的话就一直在右区间查找
if(nums[mid] <= target)
{
l = mid + 1;
}
else
{
r = mid - 1;
}
}
//注意退出循环时,l一定是在右边界的下一个位置,r在右边界的位置
j = l - 1;
return {i, j};
}
};69. x 的平方根(二分法的变种应用)
计算并返回 x 的平方根,其中 x 是非负整数。由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。输入: 8输出: 2说明: 8 的平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
思路:本题是二分查找的典型应用场景:查找一个有确定范围的整数。根据 单调性 逐渐缩小搜索范围。我们就知道了,如果一个数 a的平方大于 x ,那么 a一定不是 x的平方根。我们下一轮需要在 [0..a - 1]区间里继续查找 x 的平方根。
class Solution {
public:
int mySqrt(int x) {
//等于1或0的时候直接返回本身
if(x < 2)
{
return x;
}
int l = 0;
int r = x;
while(l <= r)
{
int mid = l + (r - l) / 2;
//用x / mid > mid代替mid * mid < x来防止溢出
//如果mid * mid小了就去右区间找
if(x / mid > mid)
{
l = mid + 1;
}
//如果mid * mid大了就去左区间找
else if(x / mid < mid)
{
r = mid - 1;
}
//相等就直接返回
else
{
return mid;
}
}
//退出循环时,l在右边,r在左边。所以要取左边的值
return r;
}
};不完全有序数组中查找
不完全有序数组最典型的例子就是旋转数组
33. 搜索旋转排序数组
整数数组nums按升序排列,数组中的值 互不相同 。在传递给函数之前,nums在预先未知的某个下标 k(0 <= k < nums.length)上进行了旋转,使数组变为[nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从0开始 计数)。例如, [0,1,2,4,5,6,7] 在下标3处经旋转后可能变为 [4,5,6,7,0,1,2] 。给你旋转后 的数组nums和一个整数target,如果nums中存在这个目标值target ,则返回它的下标,否则返回-1 。输入:nums = [4,5,6,7,0,1,2], target = 0输出:4
思路:将数组从中间分开成左右两部分的时候,一定有一部分的数组是有序的。我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid - 1] 和 [mid + 1, r] 哪个部分是有序的,并根据有序的那个部分确定我们该如何改变二分查找的上下界,根据有序的那部分判断出 target 在不在这个部分: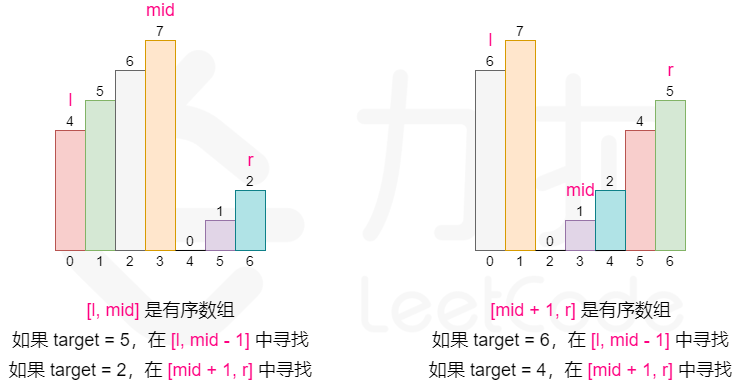
- 如果[l, mid - 1]是有序数组,且target的大小满足[nums[l],nums[mid])则应该将搜索范围缩小至[l, mid - 1],否则在[mid + 1, r]中寻找。
- 如果[mid+1, r]是有序数组,且target的大小满足(nums[mid+1],nums[r]],则应该将搜索范围缩小至[mid + 1, r],否则在[l, mid - 1]中寻找。
class Solution { public: int search(vector<int>& nums, int target) { int n = nums.size(); //特判 if(n == 0) { return -1; } if(n == 1) { return nums[0] == target ? 0 : -1; } int l = 0; int r = n - 1; while(l <= r) { int mid = l + (r - l) / 2; //如果找到target直接返回 if(nums[mid] == target) { return mid; } //中间值大于右边界,说明左区间一定有序 if(nums[mid] > nums[n - 1]) { //如果target在左区间,则在左区间搜索 if(target >= nums[0] && target < nums[mid]) { r = mid - 1; } //否则在右区间搜索 else { l = mid + 1; } } //右边有序 else { //如果target在右区间,则在右区间搜索 if(target <= nums[n-1] && target > nums[mid]) { l = mid + 1; } //否则在左区间搜索 else { r = mid - 1; } } } return -1; } };
81. 搜索旋转排序数组 II
有重复元素的旋转排序数组输入:nums = [1,1,1,1,1,1,1,1,1,1,1,1,1,2,1,1,1,1,1], target = 2输出:true
思路:对于数组中有重复元素的情况,二分查找时可能会有 a[l]=a[mid]=a[r],此时无法判断区间 [l,mid] 和区间[mid+1,r] 哪个是有序的。对于这种情况,只能将当前二分区间的左边界加一,右边界减一,然后在新区间上继续二分查找。
class Solution {
public:
bool search(vector<int>& nums, int target) {
int n = nums.size();
//特判
if(n == 0)
{
return false;
}
if(n == 1)
{
return nums[0] == target;
}
int l = 0;
int r = n - 1;
while(l <= r)
{
int mid = l + (r - l) / 2;
//如果找到target直接返回
if(nums[mid] == target)
{
return true;
}
//将当前二分区间的左边界加一,右边界减一
if (nums[l] == nums[mid] && nums[mid] == nums[r]) {
++l;
--r;
continue;
}
//中间值大于右边界,说明左区间一定有序
//此处要把nums[n-1]改成nums[r],以下同理
if(nums[mid] > nums[r])
{
//如果target在左区间,则在左区间搜索
if(target >= nums[l] && target < nums[mid])
{
r = mid - 1;
}
//否则在右区间搜索
else
{
l = mid + 1;
}
}
//右边有序
else
{
//如果target在右区间,则在右区间搜索
if(target <= nums[r] && target > nums[mid])
{
l = mid + 1;
}
//否则在左区间搜索
else
{
r = mid - 1;
}
}
}
return false;
}
};153. 寻找旋转排序数组中的最小值
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。输入:nums = [3,4,5,1,2]输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
思路:一个不包含重复元素的升序数组在经过旋转之后,可以得到下面可视化的折线图:数组中的最后一个元素 x:在最小值右侧的元素(不包括最后一个元素本身),它们的值一定都严格小于 x;而在最小值左侧的元素,它们的值一定都严格大于 x。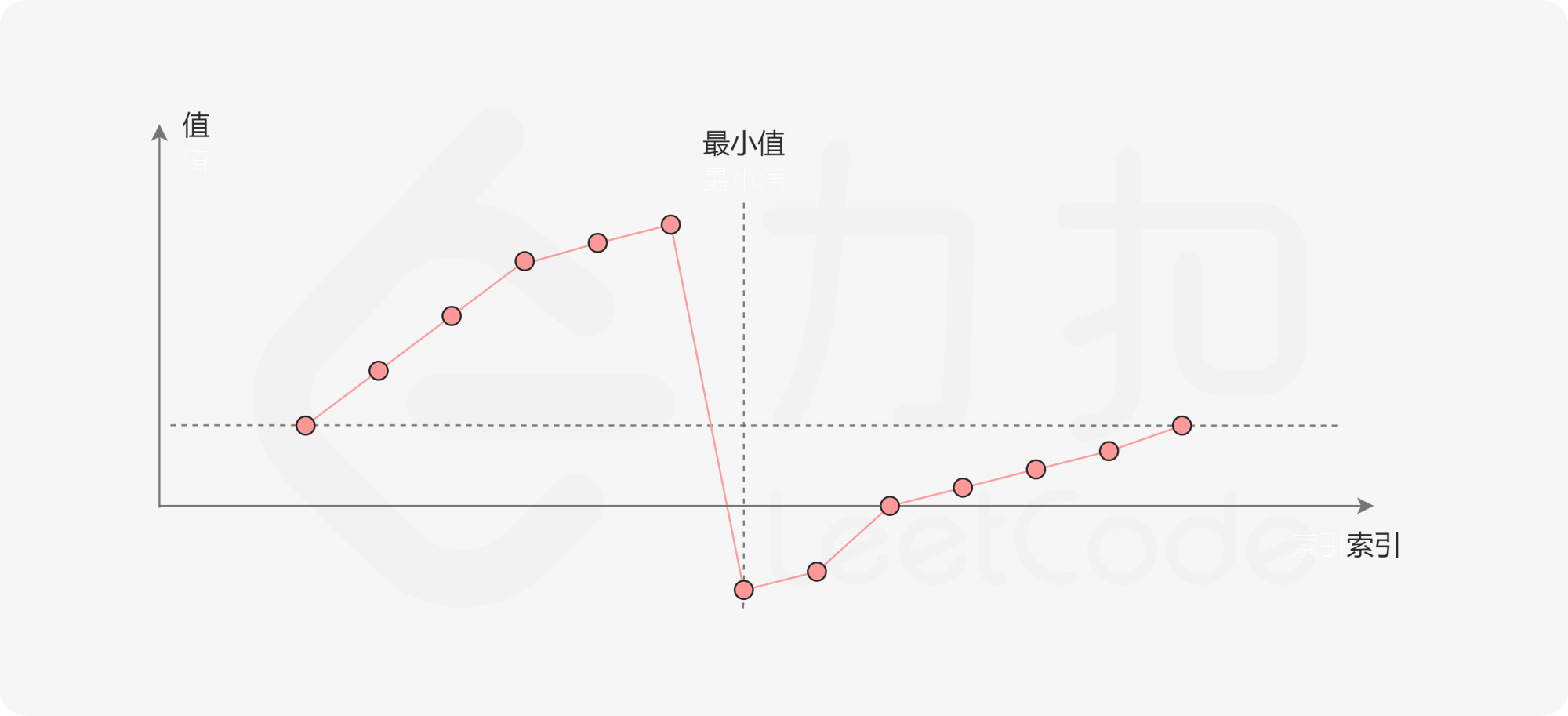
第一种情况是nums[mid]<nums[r]。如下图所示,这说明nums[mid]是最小值右侧的元素,因此我们可以忽略二分查找区间的右半部分。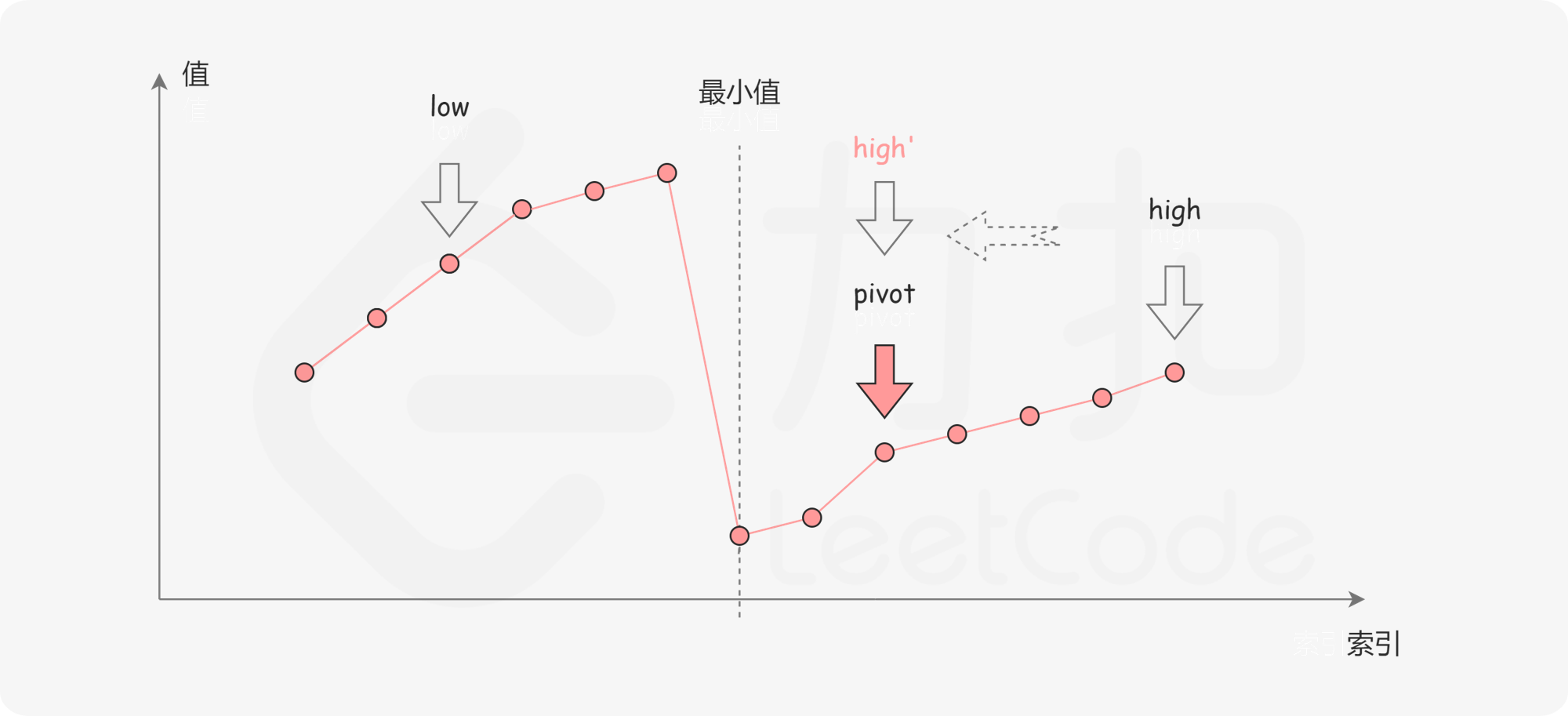
第二种情况是nums[mid]>nums[r]。如下图所示,这说明nums[mid] 是最小值左侧的元素,因此我们可以忽略二分查找区间的左半部分。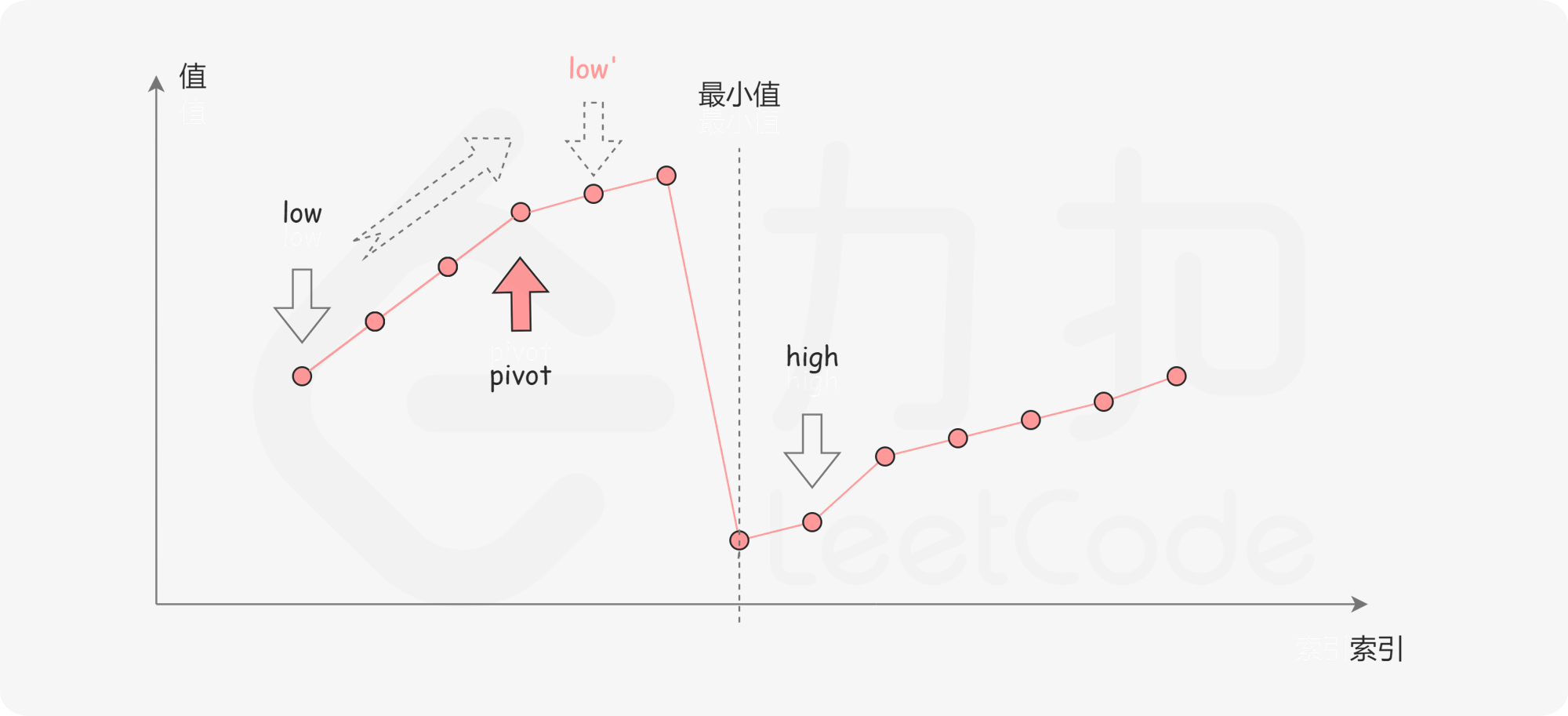
class Solution {
public:
int findMin(vector<int>& nums) {
int n = nums.size();
int l = 0;
int r = n - 1;
while(l < r)
{
int mid = l + (r - l) / 2;
//nums[mid] < nums[r],代表最小值一定在mid左侧或者就是mid,所以r移到mid的位置。
if(nums[mid] < nums[r])
{
//考虑r=mid的情况
r = mid;
}
//反之则代表最小值一定在mid右侧,将l移动到mid+1的位置
else
{
l = mid + 1;
}
}
//循环结束时,l与r重合
return nums[l];
}
};154. 寻找旋转排序数组中的最小值II
给你一个可能存在 重复 元素值的数组 nums,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的最小元素 。输入:nums = [2,2,2,0,1]输出:0
思路:本题与前一题比多了个重复的条件,因此要考虑nums[mid] = nums[r]的情况。由于重复元素的存在,并不能确定nums[mid]究竟在最小值的左侧还是右侧,不能莽撞地忽略某一部分的元素。唯一可以知道的是,由于它们的值相同,所以无论nums[r] 是不是最小值,都有一个它「替代品nums[mid],因此我们可以忽略二分查找区间的右端点。
class Solution {
public:
int findMin(vector<int>& nums) {
int n = nums.size();
int l = 0;
int r = n - 1;
while(l < r)
{
int mid = l + (r - l) / 2;
//nums[mid] < nums[r],代表最小值一定在mid左侧或者就是mid,所以r移到mid的位置。
if(nums[mid] < nums[r])
{
//考虑r=mid的情况
r = mid;
}
//反之则代表最小值一定在mid右侧,将l移动到mid+1的位置
else if(nums[mid] > nums[r])
{
l = mid + 1;
}
//相等的情况,就将右边界左移
else
{
r--;
}
}
//循环结束时,l与r重合
return nums[l];
}
};二维数组中查找
74. 搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:每行中的整数从左到右按升序排列;每行的第一个整数大于前一行的最后一个整数。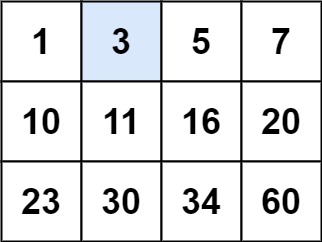
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3输出:true
思路:可以利用二分法先找到所在行,再找所在列。
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size();
int n = matrix[0].size();
int top = 0;
int bottom = m - 1;
int targetRow = 0;
//寻找目标行:最接近target并小于等于target的数
while(top <= bottom)
{
int midRow = top + (bottom - top) / 2;
if(matrix[midRow][0] > target)
{
bottom = midRow - 1;
}
else if(matrix[midRow][0] < target)
{
//记录行号
targetRow = midRow;
top = midRow + 1;
}
else
{
return true;
}
}
int left = 0;
int right = n - 1;
while(left <= right)
{
int midCol = left + (right - left) / 2;
if(matrix[targetRow][midCol] > target)
{
right = midCol - 1;
}
else if(matrix[targetRow][midCol] < target)
{
left = midCol + 1;
}
else
{
return true;
}
}
return false;
}
};总结
- 首先想清楚这道问题为什么可以用二分查找解决(而不应该先纠结二分查找该怎么写),利用题目中给出的单调性或者可以缩减问题规模的特点:已知某个猜测的答案的结果,就可以推测出比当前猜测小的时候结果如何,比当前猜测大的时候结果如何。常见应用为:有序或者半有序数组中找下标,确定一个有范围的整数。
- 首先确定搜索的范围,如果搜索的范围就把正确答案排除在外,那么是无论如何也搜不出正确结果的;
- 可以从看到的中间元素什么时候不是解开始思考 if 的语句怎么写,if的逻辑越简单越好,这样才能保证不会错,剩下的复杂的情况留给else,else的区间就是剩下的区间;
- 看到if和else里有left = mid的时候,需要将mid调整为上取整,原因是当区间里只剩下两个元素的时候,mid看到右边元素,这样落入left = mid的时候,区间才会缩减。
- 如果搜索区间里一定存在目标元素,退出while (left < right) 以后,返回left或者left代表的值就可以,否则还需要单独做一次判断;
- 不要纠结左闭右闭区间和左闭右开区间。只是要注意循环结束后各个变量所在的位置