二叉树的遍历
对于二叉树,有深度遍历和广度遍历,深度遍历有前序、中序以及后序三种遍历方法,广度遍历即我们平常所说的层次遍历。
深度遍历
二叉树的深度遍历有前序,中序以及后序三种遍历方法,具体过程如下
前序遍历:根结点 —> 左子树 —> 右子树
中序遍历:左子树—> 根结点 —> 右子树
后序遍历:左子树 —> 右子树 —> 根结点
一颗二叉树如下图所示: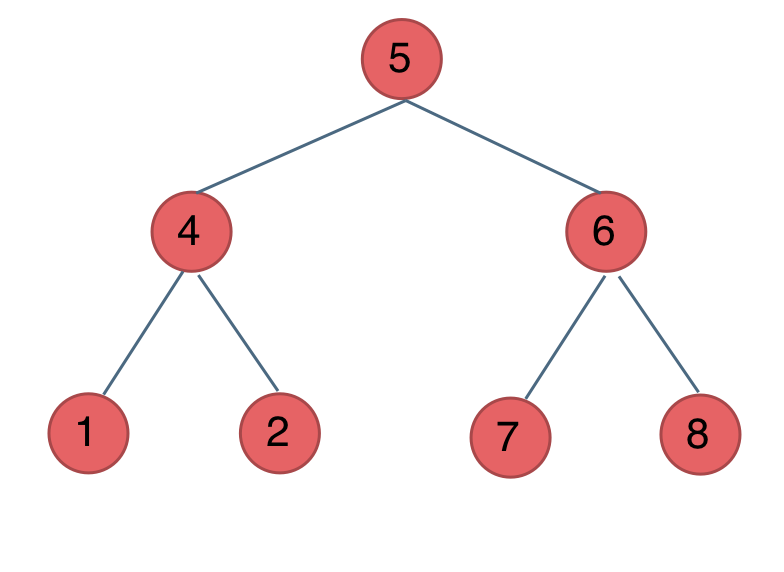
此时这棵树的:
前序遍历为[5,4,1,2,6,7,8]
中序遍历为[1,4,2,5,7,6,8]
后序遍历为[1,2,4,7,8,6,5]
深度遍历的递归法
三种遍历的题目分别为:
94.二叉树的中序遍历
144.二叉树的前序遍历
145.二叉树的后序遍历
对于递归写法,三种遍历的代码可以很容易给出:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> res;
vector<int> Traversal(TreeNode* root) {
inorder(root);
preorder(root);
postorder(root);
return res;
}
//中序遍历:左中右
void inorder(TreeNode* node)
{
if(node == nullptr)
return;
inorder(node->left);
res.push_back(node->val);
inorder(node->right);
}
//前序遍历:中左右
void preorder(TreeNode* node)
{
if(node == nullptr)
return;
res.push_back(node->val);
preorder(node->left);
preorder(node->right);
}
//后序遍历:左右中
void postorder(TreeNode* node)
{
if(node == nullptr)
return;
post(node->left);
post(node->right);
res.push_back(node->val);
}
};深度遍历的迭代法
递归的实现就是:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归为什么可以返回上一层位置的原因。
迭代的一般实现
- 前序遍历
对于前序遍历来说,前序遍历是中左右,每次先处理的是中间节点,那么先将跟节点放入栈中,然后将右孩子加入栈,再加入左孩子。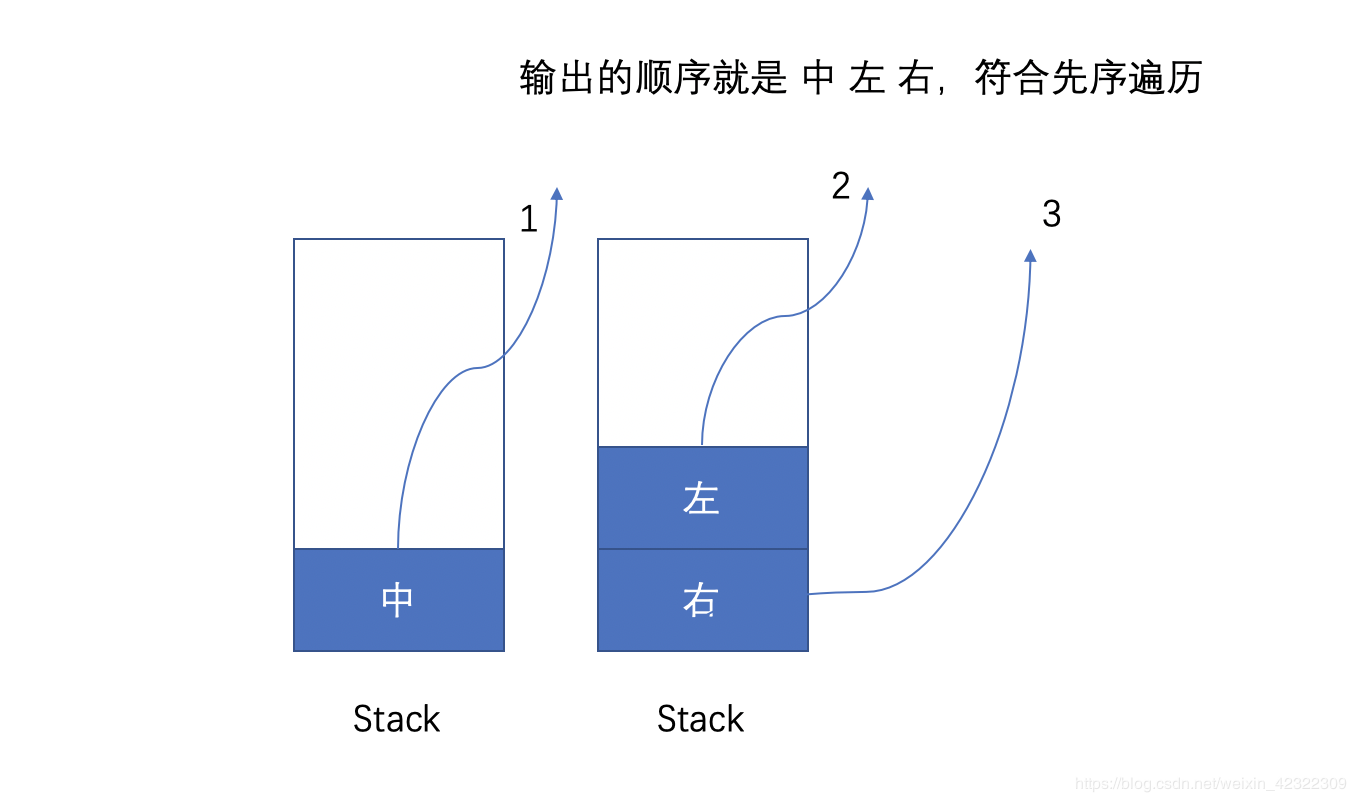
代码如下:class Solution { public: vector<int> preorderTraversal(TreeNode* root) { stack<TreeNode*> st; vector<int> result; if (root == NULL) return result; st.push(root); while (!st.empty()) { TreeNode* node = st.top(); //中间节点出栈并加入结果集 st.pop(); result.push_back(node->val); if (node->right) st.push(node->right); // 右结点入栈 if (node->left) st.push(node->left); // 左结点入栈 } return result; } }; - 中序遍历
但是对于中序遍历来说,发现不能只改变入栈顺序。这是由于:
- 前序遍历的顺序是中左右,先访问的元素是中间节点,要处理的元素也是中间节点,所以刚刚才能写出相对简洁的代码,因为要访问的元素和要处理的元素顺序是一致的,都是中间节点。
- 中序遍历是左中右,先访问的是二叉树顶部的节点,然后一层一层向下访问,直到到达树左面的最底部,再开始处理节点,这就造成了处理顺序和访问顺序是不一致的。
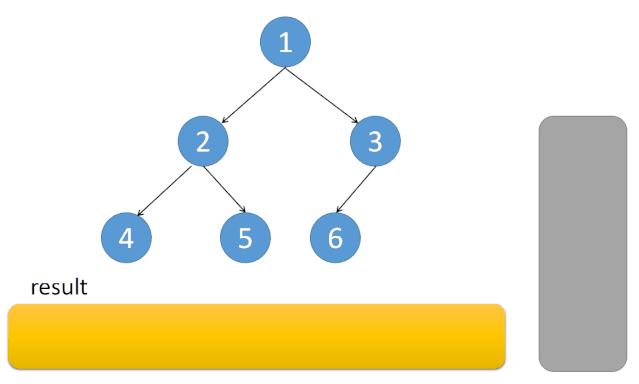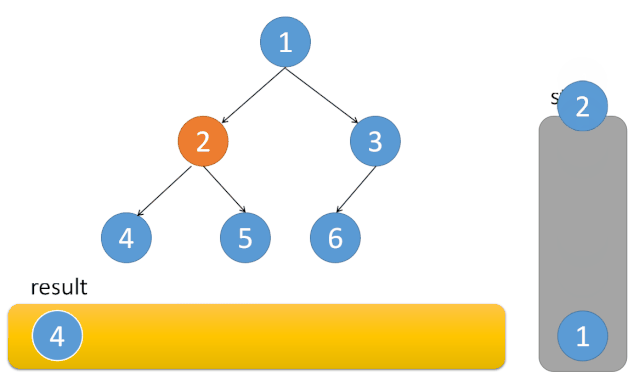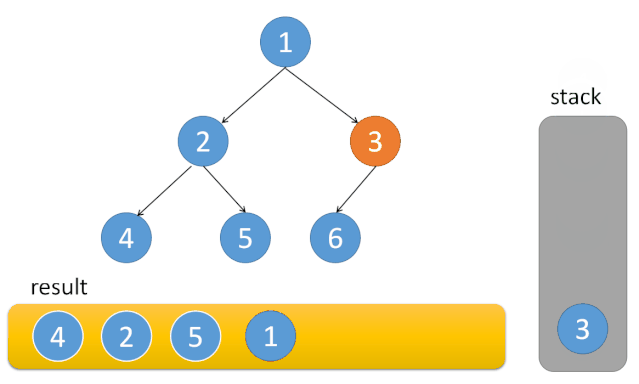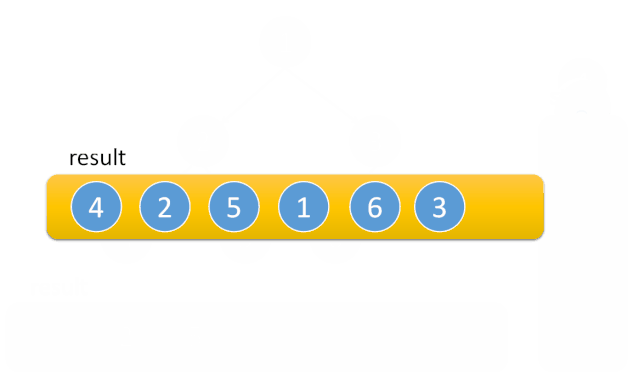
代码实现如下:class Solution { public: vector<int> inorderTraversal(TreeNode* root) { vector<int> result; stack<TreeNode*> st; TreeNode* cur = root; while (cur != NULL || !st.empty()) { if (cur != NULL) { // 指针来访问节点,访问到最底层 st.push(cur); // 将访问的节点放进栈 cur = cur->left; // 左结点入栈 } //如果指针为空 else { cur = st.top(); // 从栈里弹出的数据,放进result数组 st.pop(); result.push_back(cur->val); cur = cur->right; // 右结点入栈 } } return result; } };
- 后序遍历
再来看后序遍历,先序遍历是中左右,后续遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了。迭代的统一实现
上面的一般迭代实现中,发现风格很不统一,除了先序和后序,有关联,中序完全就是另一个风格了。而主要原因就是中序遍历中的访问节点(遍历节点)和处理节点(将元素放进结果集)不一致。
所以这一情况,就将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记 ,即再要处理的节点放入栈之后,紧接着放入一个空指针作为标记。
- 中序遍历
class Solution { public: vector<int> res; vector<int> inorderTraversal(TreeNode* root) { //遍历栈 stack<TreeNode*> stk; //先将根节点入栈 if(root != nullptr) stk.push(root); while(!stk.empty()) { //记录当前栈顶结点 TreeNode* cur = stk.top(); if(cur != nullptr) { //将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中 stk.pop(); //先添加右节点 if(cur->right != nullptr) stk.push(cur->right); //再添加中间结点 stk.push(cur); //中节点访问过,但是还没有处理,加入空节点做为标记 stk.push(nullptr); //最后添加左节点 if(cur->left != nullptr) stk.push(cur->left); } //如果遇到空结点,就处理结点(将结点放入res) else { //先将空结点弹出 stk.pop(); //取出栈中元素并加入res cur = stk.top(); res.push_back(temp->val); stk.pop(); } } return res; } }; - 前序遍历
class Solution { public: vector<int> res; vector<int> preorderTraversal(TreeNode* root) { //遍历栈 stack<TreeNode*> stk; //先将根节点入栈 if(root != nullptr) stk.push(root); while(!stk.empty()) { //记录当前栈顶结点 TreeNode* cur = stk.top(); if(cur != nullptr) { //将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中 stk.pop(); //先添加右节点 if(cur->right != nullptr) stk.push(cur->right); //然后添加左节点 if(cur->left != nullptr) stk.push(cur->left); //再添加中间结点 stk.push(cur); //中节点访问过,但是还没有处理,加入空节点做为标记 stk.push(nullptr); } //如果遇到空结点,就处理结点(将结点放入res) else { //先将空结点弹出 stk.pop(); //取出栈中元素并加入res cur = stk.top(); res.push_back(temp->val); stk.pop(); } } return res; } }; - 后序遍历
class Solution { public: vector<int> res; vector<int> postorderTraversal(TreeNode* root) { //遍历栈 stack<TreeNode*> stk; //先将根节点入栈 if(root != nullptr) stk.push(root); while(!stk.empty()) { //记录当前栈顶结点 TreeNode* cur = stk.top(); if(cur != nullptr) { //将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中 stk.pop(); //先添加中间结点 stk.push(cur); //中节点访问过,但是还没有处理,加入空节点做为标记 stk.push(nullptr); //再添加右节点 if(cur->right != nullptr) stk.push(cur->right); //最后添加左节点 if(cur->left != nullptr) stk.push(cur->left); } //如果遇到空结点,就处理结点(将结点放入res) else { //先将空结点弹出 stk.pop(); //取出栈中元素并加入res cur = stk.top(); res.push_back(temp->val); stk.pop(); } } return res; } };
深度遍历的应用
- 104. 二叉树的最大深度
输入:3/ \9 20/ \15 7输出:3
思路: 知道了左子树和右子树的最大深度 ll 和 rr,那么该二叉树的最大深度即为max(l,r)+1。
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == nullptr)
return 0;
int lDep = maxDepth(root->left);
int rDep = maxDepth(root->right);
int depth = max(leftDep, rightDep) + 1;
return depth;
}
};递归过程如下图所示: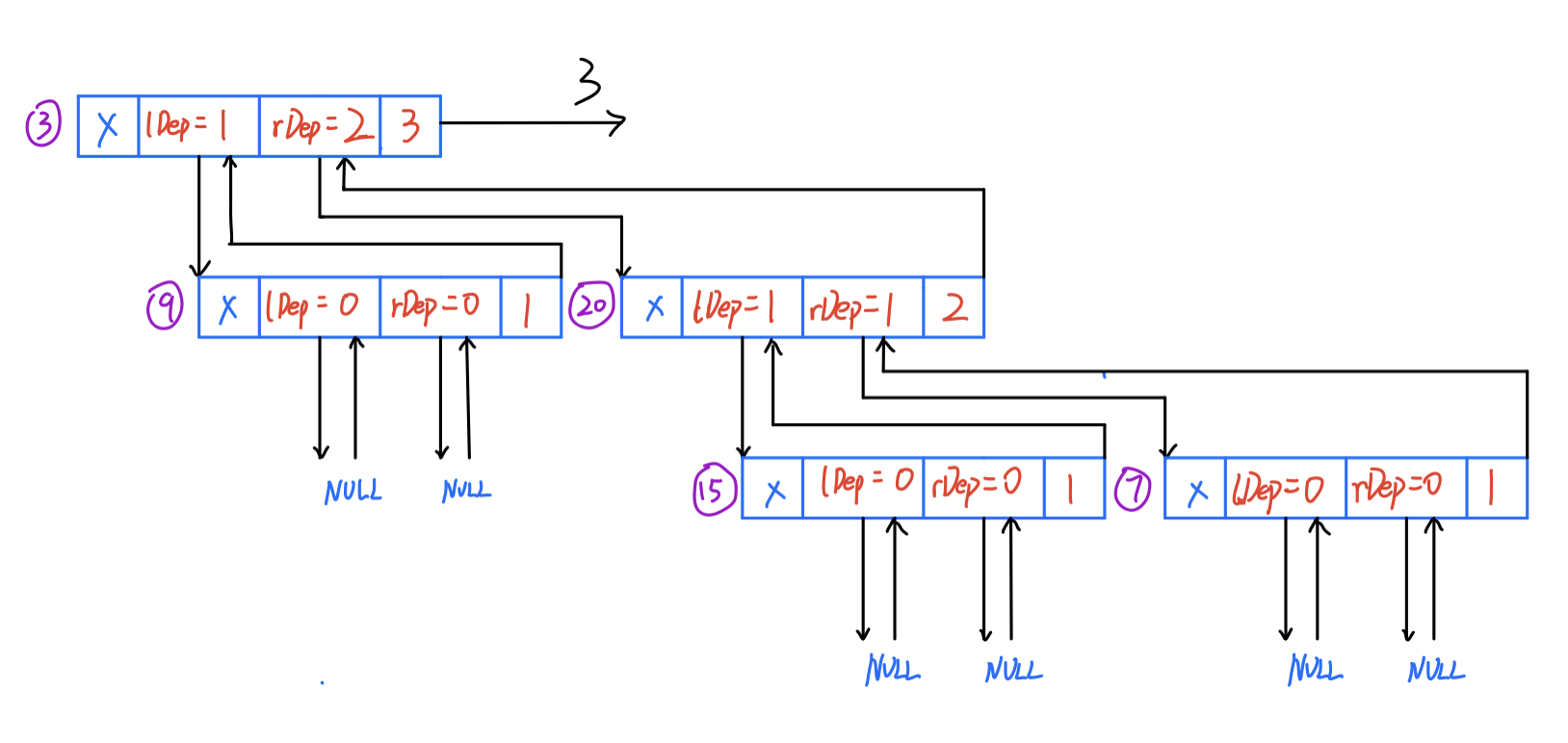
- 98. 验证二叉搜索树给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:节点的左子树只包含小于当前节点的数。节点的右子树只包含大于当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。
思路:中序遍历时,判断当前节点是否大于中序遍历的前一个节点,如果大于,说明满足 BST,继续遍历;否则直接返回 false。代码实现如下:
class Solution {
public:
long long pre = LLONG_MIN;
bool isValidBST(TreeNode* root) {
if(root == nullptr)
return true;
//判断左结点是否满足
bool leftValid = isValidBST(root->left);
if(!leftValid)
return false;
//判断中间节点
if(root->val <= pre)
return false;
//更新pre的值
pre = root->val;
//判断右节点
bool rightValid = isValidBST(root->right);
return rightValid;
}
};广度遍历
层次遍历
二叉树广度遍历的主要题型就为层序遍历:102.二叉树的层序遍历输入:[3,9,20,null,null,15,7]输出:[[3],[9,20],[15,7]]
思路:需要队列来实现,队列先进先出,符合一层一层遍历的逻辑。
class Solution {
public:
vector<vector<int>> res;
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
//先将根节点入列
if(root != nullptr)
que.push(root);
while(!que.empty())
{
vector<int> path;
//这里要固顶que的size,不然que的size一直在变
int n = que.size();
for(int i = 0; i < n; i++)
{
TreeNode* node = que.front();
que.pop();
//将结点放入res
path.push_back(node->val);
if(node->left)
que.push(node->left);
if(node->right)
que.push(node->right);
}
res.push_back(path);
}
return res;
}
};层次遍历的应用
199.二叉树的右视图输入:[1,2,3,null,5,null,4]输出:[1, 3, 4]
思路:这题就是层次遍历的典型应用,遍历时,如果为这一层的最后一个结点,就加入res
class Solution {
public:
vector<int> res;
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*> que;
if(root != nullptr)
que.push(root);
while(!que.empty())
{
int n = que.size();
for(int i = 0; i < n; i++)
{
TreeNode* node = que.front();
que.pop();
//如果是最后一个结点,加入res
if(i == n - 1)
res.push_back(node->val);
if(node->left)
que.push(node->left);
if(node->right)
que.push(node->right);
}
}
return res;
}
};


